When you imagine point potential assemblies moving through Euclidean time and space, we need a dynamical geometry that can quickly and easily calculate the electric potential and its gradients at any point in Euclidean time and space. When we compute action, we need to know the current location at absolute time Tnow and all intersecting sphere streams. The geometry must be able to compute over a single continuous path per point potential.
What is the geometrical formula for action when a point potential intersects a potential sphere? Not unsurprisingly, it relates to the Euclidean time and space position and velocity of the emitter (at emission time) and the same metrics for the receiving point potential at intersection.
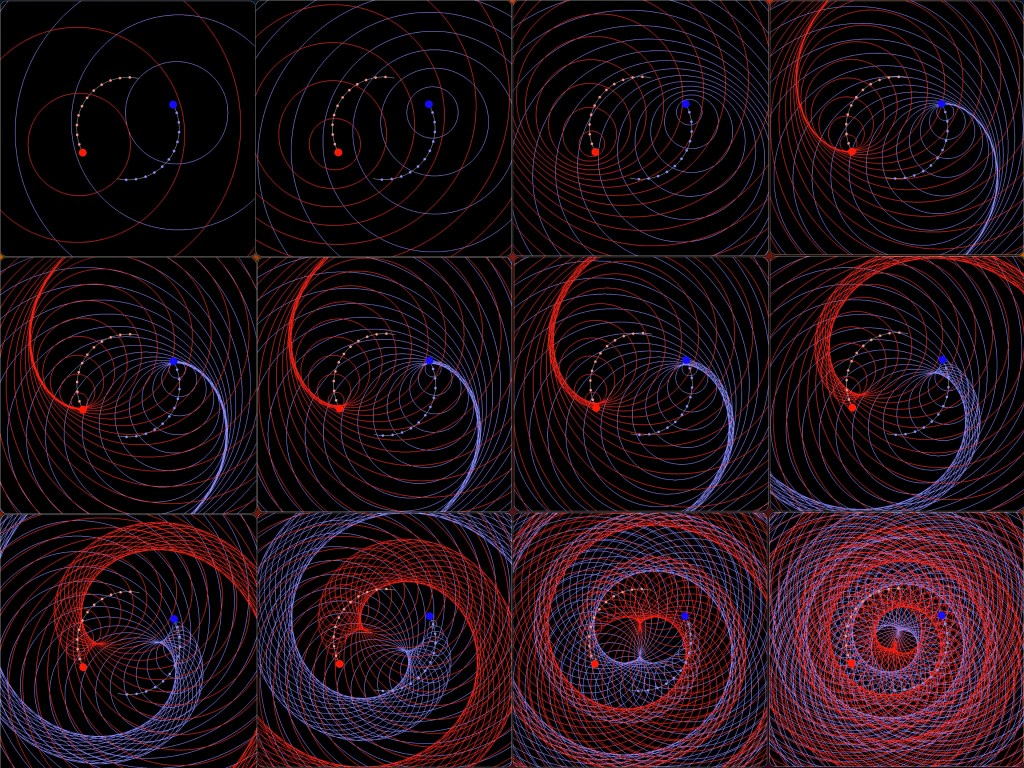
Point potential assemblies change shape and orientation depending on velocity. There are several aspects at play here. Imagine a point potential structure S with the group velocity of S being zero relative to the spacetime aether. However, the point potentials in S are executing their local path equations. Now as we perform work on S, it accelerates, and its momentum increases. This adds a velocity v component to the path of each point potential in S. The point potentials in S are also interacting, albeit lightly, with the spacetime aether local to the path. And to cap it all off, S can be reconfiguring to some degree every time it absorbs energy equivalent to an h-bar of angular momentum in the spinning Noether core. I hope this will be simple to understand with visual models and simulations.
May two (or more) point potentials occupy the same location in time and space? (esoteric?)
Let’s consider some ideal situations, each with exactly two point potentials in a void of time and space. Let’s also consider whether the two potentials are at the same (t,x,y,z) only briefly in passing or whether they could linger at the location for longer than a momentary passing.

If the point potentials are approaching on anything but an ideal line then we know that for opposite point potentials there is a maximum curvature of orbit, so any glancing contact would never spiral in on the same point in R4. There is never a case where 1/r blows up to infinity. I haven’t examined the geometry of opposite point potentials approaching, but for now I will assume that there is a corresponding asymptotic safety.
If the point potentials are approaching on an ideal line, it is not a problem because the point potential is modeled as a Dirac delta at radius = 0, i.e. q or -q. There is no radius = 0 in the denominator of a calculation. It’s not clear if point potentials could every occupy the same (t, x, y, z) position simultaneously, but perhaps it could occur in a black hole.
Note that if any two like point potentials were to ever occupy the same location for more than a passing moment, and if they had identical velocities, then it would never be possible to separate them again. Both point potentials would respond in exactly the same way to any incoming potential, were we to add more point potentials to the scenario.
If opposite point potentials were to occupy the same location, and have identical velocities, they would both continue to move on the same path going forward in absolute time. However, if we were to introduce another stationary potential somewhere in absolute space and time, then as that potential arrived the two point potentials would move in opposite directions, which would separate them.
J Mark Morris : Boston : Massachusetts