Point potentials emit spherically expanding potential at each point along their path. Spheres are characterized by their time and space origin from which we can calculate their radius. The point potentials emit at a constant rate, so the velocity of the emitter is also used to calculate the magnitude of the emission at r = 0.
Taxonomy of radius related terminology.
- r is used for the general geometrical form of r as a variable radius from an emitting unit potential to a receiving unit potential which may be itself.
- Note 1 : there are conditions where a point charge could encounter it’s own potential one or more times at a given instant t. However, each of those would have a different emission point along the path history and therefore a different r.
- Note 2 : r is only defined between path histories. No r exists unless both endpoints are a point charge, including the self.
- r-vector means a specific r with an origin and a point of action where the Dirac sphere intersects a point potential.
- r-hat means the unit radii with a length of 1 unit of distance which perhaps we can relate to the Planck length, the field speed @, and
- t-hat, the minimum unit time of binary time.
- We have a lot of flexbility here as it is only convention.
- It may make sense to bridge to Planck’s constants.
- We also know that r-hat = @ t-hat, where @ is the speed of potential.
How shall the model define the expanding emission from a unit potential? We can examine the slope and rate of change of the slope. If absolute velocity is zero, we have what seems like a static electric field decreasing spherically, however it is by no means static, it is a continuous flowing sphere stream emanating from the same origin. It is only when the point charge is moving that we introduce what science terms magnetism, but which is really a different shape to the sphere stream of each local point potential.
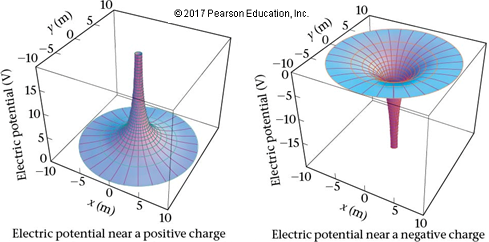
- unit negative potential : -1/r with slope 1/r2
- unit positive potential : 1/r with slope -1/r2
What information do we need to define a vector radius?
- origin : t, x, y, z along a point charge path
- elapsed time : converts to radius by r = @t
- theta and phi polar coordinates
- Alternately instead of specifying time or radius vector, one can specify the spatial coordinate t’, x’, y’, z’ where the expanding potential sphere intersects a point potential.
- Each point on a path is defined by {q, t, x, y, z, x’, y’, z’}
- Emission parameters set A = {q, t, x, y, z, x’, y’, z’}
- Receiver parameters set B = {q, t, x, y, z, x’, y’, z’}
- Action is a function of A and B. Action = f(A, B). We must consider:
- r-hat = Radial unit vector from emitter to receiver B – A. (deltas: t, x, y, z)
- R = length of radius from emitter to receiver = g(A, B)
- M = magnitude of received sphere = a function h(A, B)
- D = direction of action = k(A(q), B(q))
- must be specified relative to r-hat. Either -1 or +1.
- Vector potential is determined by M, D, R, r-hat
- It is a new way of thinking about potential.
- Potential is not a scalar at the fundamental level.
- It is very much a well-defined vector at the point of action.
- Superposition lets us to decompose that vector as we choose.
The vector potential from emission to reception is an essential concept in the dynamical geometry of point potential paths and action.
J Mark Morris : Boston : Massachusetts