I just had an insight into the figment of an idea I had several years ago. I was thinking about how the spacetime assemblies between two isolated and separated point charges would be more excited than the spacetime assemblies in any other direction. The diagram shown was made in Microsoft Excel. It shows two stationary positive point charges labeled “1” in an otherwise neutral field. I approximated the potential in each 1×1 cell using a formula based on the distance and the 1/r potential field. Using conditional shading based on the calculated values, you can visualize the saddle shape.
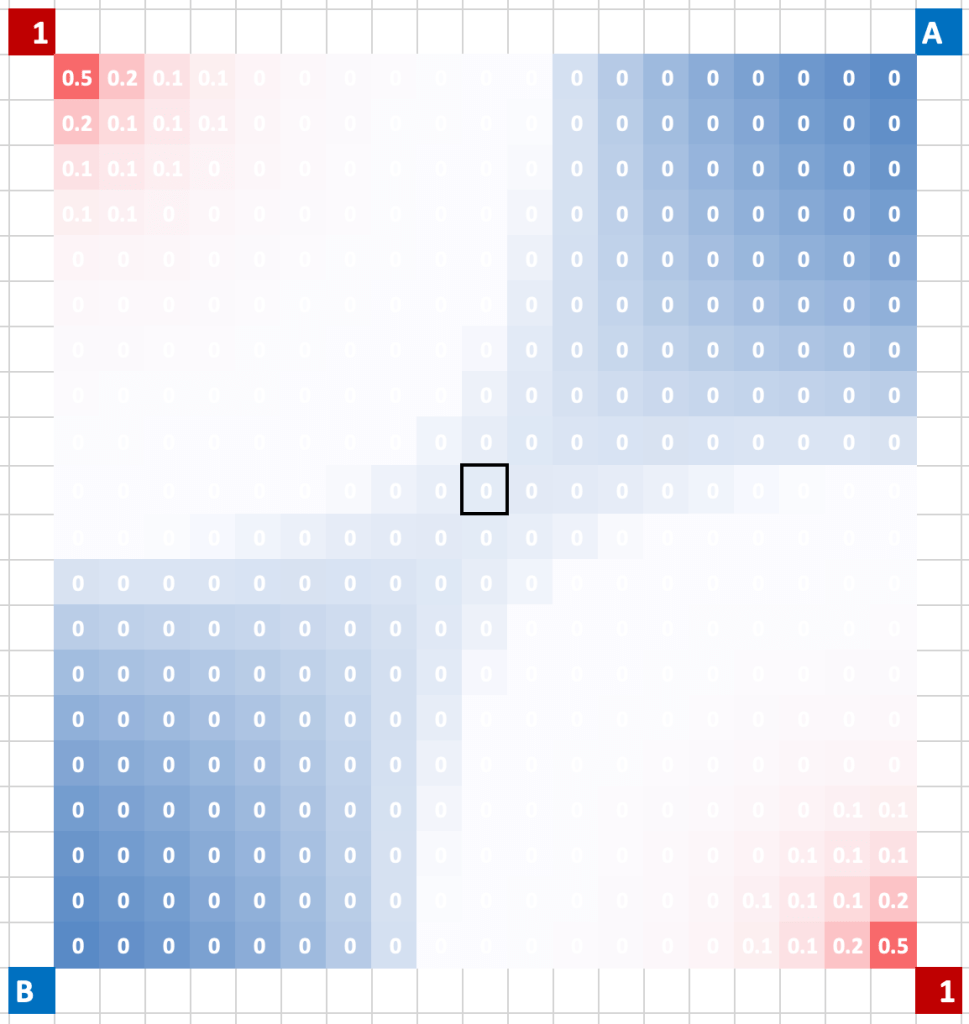
At the time, I was only thinking in terms of point charges and potential. There is a dualistic higher-level concept that dense collections of particle assemblies in massive objects (e.g., moons, planets, stars, solar systems, galaxies, galaxy clusters, etc.) and the energy they carry, will excite the spacetime assemblies that permeate everything, and which are only very lightly interactive in the sense of mass and gravity. The denser the massy object, the more excited the local spacetime assemblies become and this causes the spacetime assemblies scale to shrink.
In all of these cases there is a gradient in spacetime aether energy and dimensional scale caused by the massy objects. The gradients between two massy objects will overlap and cause an energetic channel of spacetime aether between the massy objects. All of these effects influence the paths objects in the large-scale vicinity take. The channels will collect massy objects as well.
Here is fascinating, and perhaps testable, brainstorm idea. Can we detect the geometry of the spacetime assemblies’ contraction around symmetrical objects (moons, planets, stars, etc.) and asymmetrical objects (galaxies, jetting objects, tight binaries, etc.)? Not only would this map to Einstein’s general relativity for spherical objects, but there may be research opportunities into “aura” geometry of asymmetric objects and applying that knowledge to further advancement in areas such as lensing of photons from beyond the object.
J Mark Morris : Lynn : Massachusetts
p.s. I had these insights while watching the following episode from Anton Petrov.